මාන විශ්ලේෂණය

                     මාන විශ්ලේෂණය

මාන විශ්ලේෂණය (dimensional analysis) යනු විද්‍යාවේදී බහුලව ප්‍රයෝජනයට ගැනෙන එක්තරා ගණිතමය ක්‍රමවේදයක්. විශේෂයෙන් සමීකරණ ගොඩනෑගීමට බෙහෙවින් උපකාරී වේ. මාන යනු භෞතීය ප්‍රමාණාත්මතාවයක් සංකේතවත් කිරීමට යොදාගන්න සංකේත කිහිපයකි. එය මූලික භෞතික රාශි මත පදනම් වෙයි. මූලික භෞතික රාශී 7කි. (දිග, කාලය, ස්කන්ධය, උෂ්ණත්වය, විද්‍යුත් ධාරාව, ද්‍රව්‍ය ප්‍රමාණය, දීප්ත තීව්‍රතාව) මෙහි දීප්ත තීව්‍රතාව හැර අනෙකුත් භෞතික රාශි 6 සඳහා මාන තිබේ. මාන සංකේතවත් කරන්නේ කැපිටල් ඉංග්‍රීසි අක්ෂර වලින්. නමුත් උෂ්ණත්වයේ මාන සඳහා පමණක් Θ(තීටා) ග්‍රීක අක්ෂරය යොදනවා.

[දිග] = L
[කාලය] = T
[ස්කන්ධය] = M
[උෂ්ණත්වය] = Θ
[විද්‍යුත් ධාරාව] = I
[දුව්‍ය ප්‍රමාණය] = N
මාන සමීකරණයක් ලෙස ඉදිරිපත් කරන විට අඳාළ භෞතික රාශිය කොටු වරහනක් තුළ ලියනු ලැබේ. නැතහොත් අදාළ භෞතික රාශියෙහි අදේශ කරන ලද සංකෙත්ය කොටු වරහන් තඅල ලියයි. උදාහරණයක් ලෙස a=දිග නම් [a]=L ආකාරයට ලිවිය හැක. එම වරහන මඟින් එම රාශියේ මාන නිරූපණය කෙරෙන බව හඟවයි.

                                                      යාන්ත්‍ර විද්‍යාවේ මූලික මාන ත්‍රිත්වය

මාන විශ්ලේෂණය පිළිබඳව ඉතිහාසය දෙස බැලුවොත් ජෝසප් ෆෝරියර් නම් පුද්ගලයාව අපිට හමු වෙනවා. ඔහු අයිසැක් නිව්ටන්ගේ මූලධර්ම ‍පාදක කරගෙන මාන විශ්ලේෂණ කටයුතු සිදු කර තිබෙනවා. එහිදී ඔහු මූලික වශයෙන් M, L හා T යන මාන ගොඩනැගුවා. භෞතික විද්‍යාවේදී බොහෝ වෙලාවට මෙම මාන ත්‍රිත්වය යොදාගන්නේ නිව්ටෝනිය යාන්ත්‍ර විද්‍යාව( අයිසැක් නිව්ටන්ගේ මූලධර්ම මත පමණක් පදනම් භෞතික විද්‍යාව මෙනමින් හැඳින්වේ) සඳහායි.

අපි කලින් ඉගෙනගත් SI ඒකක වගේම ව්‍යුත්පන්න භෞතික රාශි වල සූත්‍ර යොදාගෙන ඒ ඒ රාශියේ මාන සෙවිය හැක. පහත එවැනි උදාහරණ කිහිපයක් දැක්වේ.

A=වර්ගඵලය ද a=දිග ද b=පළල ද නම්
වර්ගඵලය = දිග x පළල
A = a x b
[A] = L x L
[A] = L2
F=බලය ද m=ස්කන්ධය ද a=ත්වරණය ද නම්
බලය = ස්කන්ධය x ත්වරණය
F = ma
[F] = MLT-2

‍දැන් මාන වල ලක්ෂණ ගැන කතා කරමු.

ඒකක නැති සියලුම භෞතික රාශි වලට මාන නැත.
උදා: [තල කෝණය]= චාප දිග/අරය = L/L = 1
ඒකක සහිත ඇතැම් භෞතික රාශි වලටද මාන නැත.
උදා: දීප්ත තීව්‍රතාව සඳහා කැන්ඩෙලා(cd) නම් ඒකකයක් තිබුණද මාන නැත.
සූත්‍රයක ඕනෑම පදයක දර්ශකයකට මාන නොමැත.
උදා:
N = N0e-λt සමීකරණයේ t=කාලය නම්
-λt=1
-λ = 1/t = 1/T = T-1 වේ.
එම නිසා -λt=T x T-1= 0 වේ. එවිට මාන නැත.

  මාන විශ්ලේෂණයෙහි ප්‍රයෝජන
 මාන විශ්ලේෂණයෙහි ප්‍රයෝජන (Uses of dimensional analysis) දෙකක් දකින්න පුළුවන්.

පළමු ප්‍රයෝජනය වන්නේ ‍භෞතික විද්‍යාත්මකව ගොඩ නැගූ සමීකරණයකය නිරවද්‍යතාව(සත්‍යද නොමැතිනම් අසත්‍යද යන්න) පරීක්ෂා කිරීමයි. දැන් මාන විශ්ලේෂණය යොදාගෙන සමීකරණයක නිරවද්‍යතාව පරීක්ෂා කරන අකාරය විමසා බලමු.

සමීකරණයක මාන සමාන වීම

මෙහිදී යොදාගනුයේ සරල නීතියකි. සමීකරණයක වෙන් වෙන් වශයෙන් ඇති සෑම පදයකම මාන සමාන නොවේනම් එම සමීකරණය ස්ථීරවම වැරදියි කියන්න පුළුවන්. (සමීකරණයක + හෝ – ලකුණු වලින් වෙන් වෙන කොටස් පද ලෙස හැඳින්වේ)

නමුත් සමීකරණයක සෑම පදයකම මාන සමාන වූ පමණින් එය නිවැරදි සමීකරණයක් කියා පැවසීමට බැරිය. එවිට කියනුයේ එය මාන වශයෙන් නිවැරදි සමීකරණයක් ලෙසය. එසේ වීමට හේතු සලකා බලමු.

සමීකරණයක සංඛ්‍යාත්මක නියත වලට මාන නොමැති බැවින් එම නියතයන් මඟ හැරී යාම.‍
උදාහරණ 01‍:
වර්ගඵලය=A නම් A=දිග x පළල වේ.
එවිට [A]= L x L = L2වේ.
එනමුත් A= 2 x දිග x පළල යනුවෙන් සමීකරණයක් දී ඇති විටද
[A]= L x L = L2වේ.
ඒ අනුව 2 වැනි සංඛ්‍යාත්මක නියත වලට මාන නොමැති බැවින් දෝෂය මඟ හැරී ඇත.

භෞතික රාශි කිහිපයක ගුණිතයක් ඇති අවස්ථාවක ඒවායේ වැරදි සංයෝජන වලින් සමාන මාන ලැබිය හැකි වීම.
උදාහරණ 02:
V=සිලින්ඩරයේ පරිමාවද, r=අරයද, h=උසද π යනු මාන විරහිත නියතයක්ද නම්
V = πrh2 සමීකරණයේ [V]=L3 සහ [πrh2] =L x L2 = L3 වේ. සමීකරණයේ සෑම පදයකම මාන සමාන බැවින් සමීකරණය නිවැරදි වේ.
නමුත් V = πr2h ලෙසද සමීකරණයක් දී ඇත්නම් එහි [V]=L3 ද [πr2h]= L2 x L = L3 ද වන නිසා පද වල මාන සමාන වී මෙම සමීකරණයද නිවැරදි වේ.
ඒ අනුව ගුණිතයක් ඇති අවස්ථාවක වැරදි සංයෝජන වලින් නිවැරදි මාන ලැබිය හැක.


දැන් අපි සියලු හේතූන් පැහැදිලි කරගෙන අවසානයි. පහත සමීකරණයේ නිරවද්‍යතාව පරීක්ෂා කිරීමෙන් අපිට මාන විශ්ලේෂණයෙහි මෙම ප්‍රයෝජනය ප්‍රයෝගිකව අත්හදා බැලිය හැක.

E= mgh + 1/2ρv2 සමීකරණයේ E=ශක්තියද m=ස්කන්ධයද g=ගුරුත්වජ ත්වරණයද h=උසද ρ=ඝනත්වයද v=ප්‍රවේගයද වේ නම් එම පද වල මාන මෙසේය.
[E]=ML2T -2
[mgh]=ML2T -2
[1/2ρv2] =ML-1T -2
පද තුනෙහිම මාන සමාන නොවන බැවින් සමීකරණය ස්ථීර වශයෙන්ම වැරදියි.

ඉහත පළමු ප්‍රයෝජනයේ විලෝමය යොදාගෙන සමීකරණයක මාන නොදන්නා රාශියක මාන සෙවිය හැක. එවැනි සමීකරණයක් පහත දැක්වේ.

F=BIl සමීකරණයේ F=බලයද I=විද්‍යුත් ධාරාවද l=දිගද වේ නම් Bහි මාන සොයමු.
ප්‍රථමයෙන් B උක්ත කරගත යුතුයි. එවිට B=FI / l වේ. දැන් එක් එක් රාශියට මාන ආදේශයෙන් Bහි මාන සෙවිය හැක.
[B]= MLT -2 / IL = ML-1T -2

මාන විශ්ලේෂණයෙහි තවත් ප්‍රයෝජනයක් වන්නේ සමීකරණ ව්‍යුත්පන්න(සාධනය) කිරීමේ හැකියාවයි. එනම් කිසියම් භෞතික රාශියක් රඳා පවතින කරුණූ පරීක්ෂණාත්මකව සොයාගත් විට මාන විශ්ලේෂණය යොදාගෙන ඒ සඳහා සමීකරණයක් ගොඩනැඟිය හැක. දැන් එසේ සමීකරණයක් ගොඩනඟාගන්නා අකාරය විමසා බලමු.

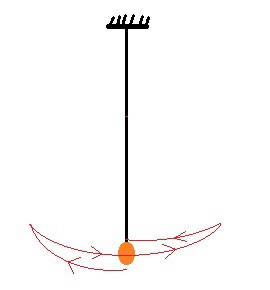
මේ සඳහා අපි සරල අවලම්බය(simple gravity pendulum) පිළිබඳ පරීක්ෂණය යොදාගමු. එනම් පහත රූපයේ ආකාරයට කුඩා ස්කන්ධයක්(කුඩා යකඩ බෝලයක්) තන්තුවකින් ගැට ගසා ආධාරකයක් මත එල්ලනු ලැබේ.

                                                  සරල අවලම්බයක දෝලනය

රූපයේ ඊ හිස් ඔස්සේ සරල අවලම්බයේ චලිතය(දෝලනය) පෙන්නුම් කරයි. එනම් නිශ්චල අවස්ථාවේදී(පොළවට ලම්බක අවස්ථාව) යකඩ බෝලයට කුඩා බලයක් යෙදූ විට දෙපසට ගමන් කරමින් පැද්දෙයි. මෙය දෝලනය වීම ලෙස හඳුන්වන අතර මධ්‍ය පිහිටීමේ සිට දෙපසට දෝලනය(oscillation) වී නැවත මධ්‍ය පිහිටීමට පැමිණීම එක් දෝලනයක් ලෙස හඳුන්වනු ලබනවා.

දැන් මේ සරල අවලම්බය මත ක්‍රියා කරන භෞතික රාශී මොනවාදැයි බලමු. දෝලන කාලය, තන්තුවේ දිග සහ යකඩ බෝලය පහළට ඇඳ තබා ගන්නා ගුරුත්වජ ත්වරණය(acceleration of gravity) යන රාශින් ත්‍රිත්වය මත ‍සරල අවලම්බයේ දෝලනය රඳා පවතින බව අපට නිරීක්ෂණය කළ හැක. ඒ අනුව මෙහි දෝලන කාලය T ලෙසද තන්තුවේ දිග l ලෙසද ගුරුත්වජ ත්වරණය g ලෙසද ගනිමු.

T, l මත රඳා පවතින බැවින් එම රාශීන් දෙක සමානුපාතික වේ. එනම්,
T ∝ lx වේ.

T, g මතද රඳා පවතින බැවින් එම රාශින් දෙකද සමානුපාතික වේ. එනම්,
T ∝ gy වේ.

ඒ අනුව T, l සහ g මත රඳා පවතින නිසා මෙසේ ලිවිය හැක.

T ∝ lx gy
T = k lxgy

මෙහි k යනු මාන රහිත නියතයකි. සමානුපාතිකයක් සමීකරණයක් බවට හැරවීමේදී නියතයක් යෙදිය යුතු වේ. දැන් මාන විශ්ලේෂණය යොදාගෙන x සහ y සොයාගත යුතුයි.

කලින් උගත් පරිදි T හි මාන T ලෙසත් lහි මාන L ලෙසත් gහි මාන LT -2 ලෙසත් ගනිමු. ඉන්පසු පෙර තනාගත් සමීකරණයට ඒවා ආදේශ කරගත යුතුයි. සමීකරණයේ දෙපසටම සාධාරණ ලෙස මාන යෙදිය යුතුයි. ඉන්පසු සමීකරණය සුළු කරගෙන x,y ලබාගත යුතුයි.

L0 T1 = Lx (LT -2)y
L0 T1 = Lx Ly T -2y
L0 T1 = Lx+y T -2y

-2y=1
y= -1/2

x+y=0
x+(-1/2)=0
x= 1/2

x=1/2 සහ y=-1/2 ආද්ශයෙන්
T = k lxgy
T = k l1/2g-1/2
T = k l1/2 / g1/2

දැන් අපි සමීකරණය ගොඩ නඟා අවසන්. තවද මෙහි නියතය 2π බව සොයාගෙන ඇත. එමනිසා පහත පරිදි සමීකරණය ලිවිය හැක.

                                   

අපි ගොඩනගන ලද මේ සමීකරණයට පාදක පරීක්ෂණය සුප්‍රකට ගැලීලියෝ ගැලීලියෝ විද්‍යාඥයා විසින් කරන ලද්දක්. ඔහු කළ සරල අවලම්බ පරීක්ෂණය සඳහා සමීකරණයක් තමයි අපි විසින් දැන් මාන විශ්ලේෂණය යොදාගෙන සාධනය කලේ.

ඉතින් මෙසේ පරීක්ෂණාත්මකව ඔප්පු කිරීම් සඳහා මාන විශ්ලේෂණය යොදා ගන්නවා. කිසියම් පරීක්ෂණයකදී භාවිතා වන භෞතික රාශීන් දන්නේම් ඒ ඔස්සේ අපිට සමීකරණ ව්‍යුත්පන්න කරගත හැක